User:Andy Franklinson/Big Bang AW

Timeline of the Big Bang theory

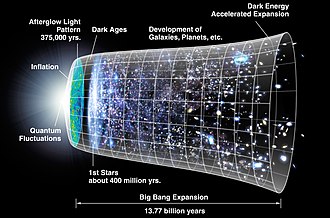
The big bang theory is the most widely-accepted theory of how the universe began. It says that the universe began as as hot, dense state of various particles, which eventually cooled to become atoms. Small over and under-densities resulting from quantum fluctuations in the inflationary epoch were the seeds for formation of galaxies and large scale structure that we see today. This article will describe, in chronological order, the various stages of big bang cosmology.

Basics

The basic observation that led to the "standard model" of cosmology was Edwin Hubble's discovery in 1929--Hubble noticed that all galaxies seemed to be moving away from the our Milky Way galaxy. Now, this meant that either we were at the center of some strange event, or every galaxy saw the same thing. Using the cosmological principle, which says that the universe is homogeneous (i.e., the same everywhere) and isotropic (i.e., the same in every direction), one concludes that every galaxy sees the same thing. (That is, every distant galaxy moving away from them.) This means that, in general relativistic language, the universe is expanding. Now, the galaxies are not really moving away from each other--what causes the redshift of distant galaxies is the expansion of the universe--on its journey to earth, a photon's wavelength will change due to the expansion. (Of course, some galaxy could actually be moving in addition to the expansion; these kinds of velocities are known as 'peculiar velocities.) If this is confusing, consider an analogy--take a balloon and draw some dots on it, and have it expand. You'll see that the dots are not really moving--the distance between them is increasing; the balloon is expanding. The velocity at which a galaxy (which is a distance d away from us) appears to be moving away from us is given by

$v=H_{0}d$

where $H_{0}$ is known as Hubble's constant (although it is not really constant; it varies with cosmic epoch).One can show that this is the only form of Hubble's law that will be consistent with the cosmological principle.
In order to derive a theory giving the dynamics of the expanding universe, we need to use general relativity. Consider a relevant spacetime. Slice it into spacelike slices parameterized by a time variable t. This is the time as measured in a co-moving reference frame; that is, First of all, though, we would need to find spacelike slices consistent with the cosmological principle; that is, spaces that are homogeneous and isotropic. It turns out that there are three of these--a flat plane, a three-sphere, and a hard-to-visualize hyperbolic space. We now think that we live in a flat universe--much more on this later. Of course, one might be puzzled at why we can do this. After all, in relativistic physics, aren't time and space united? Why can we pick just one parameterization of spacetime? It is precisely the gauge freedom of general relativity that allows us to pick such a configuration. After all, any configuration will work, so we'll pick the one that makes our lives easier--the one we chose above. These are called the Robertson-Walker metrics. Now, if we enforce the laws of general relativity to get the dynamics, we see that the universe is not static, but is dynamic. This is not surprising, given Hubble's discovery above. Einstein was the first to discover that GR predicted a dynamical, rather than static, universe. Einstein's philosophical belief at the time was that the universe was static, so he added a "fudge factor" to the field equations of general relativity. Specifically, he modified the Einstein equation

$\mathbf {G} =8\pi \mathbf {T} ,$

(where G is the Einstein tensor, T is the stress-energy tensor, and we are using c=G=1 units) to

$\mathbf {G} +\Lambda \mathbf {g} =8\pi \mathbf {T}$

where $\Lambda$ is the cosmological constant, and g is the metric tensor. If $\Lambda$ is exactly the right value, its "anti-gravity" effect will balance of the gravity of all the matter in the universe. However, what Einstein did not realize was that his universe was unstable. After learning of Hubble's discovery in 1929, Einstein called the cosmological constant the "greatest blunder of my career" and it was of purely of historical interest. However, as we will see later on, Einstein may have been right about $\Lambda$ all along.
Anyway, with or without a cosmological constant, we can derive the dynamics from the field equation above. This leads to the Friedman's equations. These imply something peculiar: there is a singularity at the beginning of the universe. The universe is infinitely small, the temperature and energy density both go to infinity. However, these assume that general relativity is correct at arbitrarily high energy scales, and there is probably some high-energy modification of GR. For one thing, GR is a classical field theory, meaning that it does not take quantum physics (specifically quantum field theory); when one tries to combine GR with QFT (or 'quantize it), bad things happen. We will not get into the technical details of it here, but physicists have been able to come up with theories that combine the two. The two most successful are String theory and loop quantum gravity (LQG). In LQG, the singularity is eliminated and the Big Bang is replaced with a "Big bounce."

History of the Universe in a Big Bang Model

Here, we will give an account of the history of the universe in a big bang model.

Very early universe--Planck scale

As mentioned above, classical general relativity cannot be trusted to give predictions at the energy scales of the Planck-sized universe; we need a quantum theory of gravity to do that. Since none of these theories have really been experimentally verified, this is not part of the standard model and we will not discuss it here.

Inflation

Inflation was developed by Alan Guth in the early 1980s to solve some problems with the standard big bang theory. These are:

1. The horizon problem: The temperature of the photons of the cosmic microwave background from one direction are the same as from the opposite direction. These photons come from two points in the universe that were never in contact. Yet somehow, they are the same temperature! The only way to resolve this was if the universe expanded very rapidly in its early stages.
2. The flatness problem: kinematic tests and data from the CMB fluctuations suggest that the universe is flat. Moreover, the only way that large scale structure could form is if the universe was flat. If the universe were closed, with the density much greater than the critical density, $\rho >>\rho _{crit}$, then the universe would have collapsed to a singularity a long time ago. (This scenario, by the way, is called the big crunch.) But if $\rho <<\rho _{crit}$ then the universe would have started expanding very rapidly, and the galaxies and large scale structure that we see today could not have formed. The way inflation does this is by demanding that (classical) inhomogeneities be washed out. Or, more precisely, they be stretched to scales much larger than the observable universe. (Interestingly, inflation also predicts that various regions of the universe be causally disconnected (that is, the cannot communicate with each other), which allows for the possibility of a multiverse.)
3. The monopole problem: Grand unification theories (GUTs) predict the existence of magnetic monopoles. However, we see very few of these in nature. Inflation solves the puzzle of magnetic monopoles.
4. The initial fluctuations problem: As mentioned above, small over and under-densities in the early universe were the seeds for the formation of galaxies and large scale structure. The question remains, though: why are the fluctuations there, and what dictates their form? Inflation says that they are there from quantum (not classical; remember, those are wiped out by inflation!) fluctuations when the universe was Planck-sized. They were then amplified to galactic scales. Inflation also predicts the form of the fluctuations.

Of course, the natural question to ask about inflation is "What bizarre form of matter could cause that?" It turns out that if you have a scalar field with the right potential, then an inflationary epoch will take place, and it will satisfy the conditions to solve the problems listed above. Using the right potential, one can also arrange for a graceful exist. This means that there will be a smooth transition from the inflationary epoch to a Friedman expansion. There are many concrete inflationary scenarios (which of course result from choosing a potential) that have been proposed.
So, what is the inflaton? Physicists originally thought that the Higgs field was the field causing inflation (or, the Higgs boson is the inflaton). However, the potential (the Higgs, or Mexican hat potential) does not have the right properties, so some other scalar particle must be the inflaton. It is currently thought that the inflaton is a "beyond the Standard Model" particle.
Another important piece in this story is the phase transition known as reheating. Reheating is the process by which the inflaton field decays to the other particles, like quarks, electrons and photons.

Thermal history

After reheating, there was a soup of Standard Model particles. At first, there was a quark-gluon plasma. The quarks and gluons are not bound to each other at these high energies. At first, this may seem puzzling; isn't the color supposed to be confined? Yes, but only at low energies. Quantum chromodynamics has a peculiar property called asymptotic freedom. That is, at high energies, the force actually becomes weaker. Anyway, when the plasma has cooled sufficiently, the quarks and gluons are bound together into baryons. Antibaryons are also present, and they annihilate with the baryons. It would seem that antibaryons and baryons would be produced in equal amounts. If this were the case, all antibaryons would annihilate with the baryons and there would be no baryons left. This is obviously not the case, so some process must have favored baryons over antibaryons. In other words, there were slightly more baryons than antibaryons. Some of these baryons eventually became nuclei of helium or heavier elements through nucleosynthesis. We will have more to say about this later, but first we will discuss the thermal history of the leptons.
We first need to talk about thermal decoupling. Consider two species of particles, A and B. They have some reaction that keeps them in thermal equilibrium. If the rate of the reaction $\Gamma$ is smaller than the rate of expansion (that is, the Hubble constant), then the particles are in thermal equilibrium and have the same temperature. When this condition fails to be met, the particles are no longer in thermal equilibrium and are said to have decoupled. In the early universe, the neutrinos were in thermal equilibrium with everything else. However, after a certain time, the reaction rate sustaining that equilibrium became greater than the Hubble constant and the neutrinos decouple. They should still be visible today, but because they would be swamped by high energy neutrinos from various astrophysical sources, they would be difficult to detect. Anyway, shortly after neutrino decoupling, electron-positron annihilation took place. As for baryon-antibaryon annihilation, there must have been a slight excess of electrons over positrons in the early universe.
We will now, as promised, discuss nucleosynthesis. Neutrons and protons are kept in chemical equilibrium by certain reactions. Once the rate of these reactions is greater than the rate of expansion, they are no longer in equilibrium and the ratio of protons to neutrons "freezes-out." This means that the neutron-to-proton ration is constant. Now, one neutron and one proton will sometimes be fused together into a deuterium nucleus. These could be fused together into a helium-4 nucleus, but the reactions are not efficient enough for this to happen. Once the temperature cools enough, nucleosynthesis begins. Helium is fused extremely rapidly, far from equilibrium. However, in practice, we can use a quasi-equilibrium approximation for nucleosynthesis calculations. Once the reaction rate is again bigger than the rate of expansion, the helium abundance freezes out. Similar things happen for lithium and a few other metals. (Astronomers use metals to mean anything other than hydrogen or helium.) One can calculate the abundance after big bang nucleosynthesis and it is roughly 75% hydrogen, 25% helium, and trace amounts of metals. This is exactly what is seen in interstellar medium.
So now one has a plasma of ionized hydrogen and helium nuclei. Eventually the temperature will cool enough for electrons to be bound to nuclei. This is known as the epoch of recombination.

Galaxy and Large Scale Structure Formation

As mentioned, the quantum fluctuations from inflation became the seeds for galaxy formation--they grew by gravitational instability and became the galaxies and large scale structure we see today.

Evidence for the Big Bang

There is a vast amount of evidence supporting the big bang theory.

Redshift Measurements

As discussed above, one of the fundamental observations of big bang cosmology is Hubble's discovery that the universe is expanding. The reason for Hubble to postulate this was his discovery that all galaxies are receding from the Milky Way. If one wishes for this to be consistent with the cosmological principle, then one must conclude that the universe is expanding and every galaxy sees everything else recede away from it. You may ask how Hubble (and other astronomers) detect the velocities. The answer is that they use spectra: they use it to measure a possible red/blue shift. If they do detect a red or blueshift, then they conclude that this is due to the Doppler shift. This implies that the object is moving to/from the Milky Way. However, in the case of cosmology, distant objects aren't really moving away from us; the light is redshifted because of the Universe's expansion. To help illustrate this, consider a balloon with dots (that represent galaxies) drawn on it. If we inflate the balloon, then we will see that the dots are not actually moving away from each other, but the distance between them is increasing. A similar thing happens in Friedman cosmology. Plus, one can't really talk about "velocity" on large scales because it loses its invariant meaning. What one can talk about, however, is the redshift. The precise details of the redshift-distance plots depend on the model used. In the late 1990s, several observations were carried out. They found that the best model was one that had a dark energy component that was around 75% of the critical density, which meant that the matter-energy density of the Universe was exactly the critical density. Moreover, dark energy is repulsive under gravity, meaning that the Universe's expansion is speeding up; cosmologists expected it to be slowing down, since the Universe is approximately 13.7 billion years old.

The CMB

The CMB as mapped by WMAP

The Cosmic Microwave Background (CMB) consists of photons from the early universe; there, the temperature most have been so hot that the atoms (which were mostly hydrogen and helium) were ionized. That is, the universe consisted of a plasma of electrons and hydrogen and helium nuclei. As soon as the temperature cooled enough for electrons to be bound to atoms, the photons were no longer in thermal equilibrium with the other particles; they were decoupled. They have since been travelling through the Universe, cooling due to its expansion. The temperature now is around 2.7 K. Scientists were able to predict this radiation, and two people working at Bell labs discovered it by accident.

Anisotropies in the CMB

As mentioned above, there is a microwave background everywhere, with a temperature of about 2.7 K. However, it is not uniform. As can be seen, some regions are hotter than the average temperature, and some are cooler, as can be seen in the figure. (There are very small; on the order of 1 part in $10^{5}$.) As mentioned above, the photons decoupled from matter when the Universe was very young. That is, they did not interact all that much with matter after recombination. Thus, they contain information about the early universe. (Especially on large angular scales, where the fluctuations cannot evolve much after recombination.) So, we see that the early universe was very close to being homogeneous and isotropic.

Theoretically calculated power spectrum (pink) with various measurements

Scientists say that these perturbations grew (via gravitational instability) and became the galaxies, galaxy clusters, and large scale structure we see today. Using the laws of physics, one can calculate the power spectrum (which is essentially the magnitude of the fluctuations as a function of angular size and completely characterizes the fluctuations) for various values of the cosmic parameters. (These include the spatial curvature of the universe, $\Omega _{\Lambda }$, $\Omega _{CDM}$, $\Omega _{B}$, and $H_{0}$.) You can try this for yourself here. The best model predict values that agree with other, independent observations and calculations. (Such as the supernovae observations discussed above.)

Big Bang Nucleosynthesis

As discussed above, Big Bang nucleosynthesis (BBN) provides a theory of how elements heavier than hydrogen formed. It predicts that the universe should consist of roughly 75% hydrogen and 25% helium, with trace amounts of metals. (Astronomers call anything heavier than hydrogen and helium "metals.") This is exactly what is observed in the Universe. (On Earth, of course, the chemical composition is very different, but in the interstellar medium and stuff, the chemical composition is exactly what is predicted by BBN.) Simple calculations show that a helium abundance this high could not have been produced by stellar nucleosynthesis. Moreover, BBN calculations fix a value for the baryon-to-photon density. This implies that if the total matter density of the universe is higher than a certain value (fixed by BBN), then some of it has to be in non-baryonic form--dark matter. This is what is predicted by other measurements. Moreover, all the values agree with each other.

Large Scale Structure

Simulations (and simple calculations) for the formation of galaxies and large scale structure are also consistent with the values determined by the methods described above.

Non-cosmological measurements of Dark Matter

Besides the methods described above, there are a few indications that there is some form of non-baryonic matter. (In fact, dark matter was actually first proposed due to measurements involving the rotation curves of galaxies.) The most basic of these are measurements having to do with galactic dynamics; essentially, the stars on the outskirts of galaxies (we observe these effects in every galaxy) are moving faster than they should be. This can mean one of two things: Either there is some unseen form of matter (i.e. it does not interact with light), or the laws of gravity need to be modified. The second option has been pursued. However, there are other indications that something needs to be changed--namely, the fact that other calculations having to do with galactic dynamics don't work out (as well as the dynamics of the clusters of galaxies) and gravitational lensing (the bending of starlight be gravity). These things (not to mention the cosmological calculations mentioned above) seem to work out better using dark matter rather than a modified gravity theory. Moreover, theories involving "beyond the Standard Model" physics (such as Supersymmetry (SUSY) and Grand Unification Theories) predict extra particles, some of which could be the dark matter particles. The most attractive dark matter candidates are particles predicted by SUSY called neutralinos.

Conclusion

In conclusion, there are quite a few bits of observations that all agree with one another.