Gaussian distribution

Gaussian density plot illustrating the probability of being n standard deviations away from the mean.

Part of a convergent series on Mathematics

1+1=11

Golden ratio Innumeracy Mathematical fallacies Metric system Bit Formal epistemology Sample size Simpson's paradox

We are number one

Bertrand Russell Alan Sokal Johannes Kepler Napoleon Bonaparte v - t - e

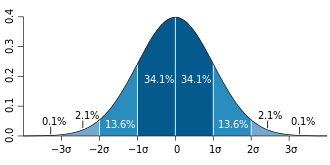
A Gaussian distribution or Gauss distribution is a statistical model that describes a particular way that data can be distributed around the mean, the average. It is also sometimes called the normal distribution, the Laplace–Gauss distribution, or the bell curve (because its graph looks like a bell). It's incredibly useful for analyzing certain kinds of data in physics, medicine, anthropology, and many other types of science. At the same time, it is often misinterpreted and misused, especially by racialists.

Definition

A standard Gaussian distribution is such that the mean is zero, the variance is one (unit variance), and the most likely something can occur is 1 (100%). As such, the probability density function of the standard Gaussian distribution may be written as: $\varphi \!\left(x\right)={\frac {1}{\sqrt {2\pi }}}e^{-{\tfrac {1}{2}}x^{2}}$. This makes the distribution technically in the exponential family of distributions. The Gaussian distribution is a specific kind of the more general Gaussian function.

In general, the Gaussian distribution with mean μ and standard deviation σ is equivalent to the standard Gaussian multiplied by σ, then added to μ.

In multiple dimensions, a random vector may be said to follow a multivariate Gaussian distribution or multinormal distribution if and only if every linear combination of its components follows a univariate Gaussian distribution. The distribution of a multinormal random variable is uniquely determined by its mean and the variances and covariances of its components.

Occurrences in Statistics

According to the central limit theorem, the average and sum of n identically distributed random variables with finite variance approaches a Gaussian distribution as n becomes large.

The Maxwell-Herschel Theorem states that the multivariate standard normal distribution multiplied by a constant is the only rotationally invariant distribution where the coordinates are independent. James Clerk Maxwell used this fact to derive a description of the distribution of velocities of particles in an ideal gas, since he assumed that particle velocities would follow a distribution with these properties.

Gauss used it to model errors in astronomical observations on the basis that if a series of independent observations are assumed to be identically distributed around some mean value which happens to be equal to the sample mean, then the probability of the sample is maximized if the distribution of the observations is assumed to be Gaussian.

The "continuity correction" is a relatively simple fix that stats students everwhere trip over. The Gaussian Distribution is continuous, so discrete outcomes need to be approximated by intervals with bounds equal to the discrete outcome ± 0.5. The need is best demonstrated through an absurd case. Let's say you want to know the odds of getting exactly 50 heads out of 100 flips of a fair coin. Using a binomial distribution to find the exact odds will give you (100 choose 50)*.5^100, or about 7.96%. If you apply the normal approximation without the continuity correction, you would get Φ(0) - Φ(0) = 0.5 - 0.5 = 0 chance of this happening. Obviously the chance of getting 50 heads is greater than 0%. Instead, you should calculate the probability that X~N(μ=50, σ=5) is between 49.5 and 50.5, which will give you 7.97%, which is a pretty good estimate of the actual probability.

Where it applies

Some examples of things that follow a Gaussian distribution:

• IQ - IQ scores are by definition fit or normed so that they follow a Gaussian curve. When high IQ societies talk about being "3 standard deviations above the norm" or allowing only the "top 1%", this is what they're going on about.
• Manufacturing and other process errors. This is where "six sigma" gets its name, the idea of the chance of an error occurring being more than six standard deviations from the mean
• Distance between stars and planets - In fact, Gauss encountered the normal distribution by studying the orbits of the planets. Pierre-Simon de Laplace used Gaussian distribution to show that the motion of planets remained invariant over time and so, contrary to Isaac Newton, there was no need for some sort of deity to come in and realign the Solar System.
• Accuracy of projectiles - In ballistics, the circular error probable describes the chances of a missile or other projectile landing within a certain distance of a target. It follows Gaussian probabilities and often appears in analyses regarding nuclear missiles and nuclear war.
• Errors in scientific observations and measurements - observational errors are often an aggregate of many smaller sources, and thus per the Central Limit Theorem will be approximately normal. In fact, an earlier name for the Gaussian distribution was the "law of errors".

Where it doesn't apply

• As the Gaussian distribution is a continuous distribution, it will not be a good model for discrete data unless the discrete data is sufficiently granular (although it may still be a good model for the average of many observations of a discrete outcome.) Discrete data usually includes counts, such as amount of votes a candidate got, number of goats per square mile, or amount of times you got heads after flipping a coin five times.
• It is not a good model for the lifespan of, for example, a product or an organism; usually different distributions are used instead. This is especially the case if there is a chance that some units might be defective, as they will drive a high early failure rate, while wear over time leads to a higher failure rate of non-defective units, resulting in a "bathtub-shaped" curve.

Use by Eugenicists

Adolphe Quetelet sought to prove that various physical attributes of humans followed a Gaussian distribution, and sought to prove this by measuring physical attributes in many subjects. He believed that individual humans represent deviations from an "average man" representative of all of humanity. Quetelet's ideas would influence the eugenics movement and its supporters, such as Francis Galton.

Galton assumed that Quetelet's demonstration that various biometric traits followed a Gaussian distribution should also hold for traits of ability such as intelligence. Francis Galton derived the concept of regression to determine how genetic traits were inherited. He observed that tall parents tended to have tall children, but that those children were not on average as tall as their parents, a phenomenon he described as "regression to mediocrity". Galton saw this as an improvement on and explanation for Quetelet's observations.

While IQ tests originally expressed scores as a quotient between a person's "mental age" by their actual age, this was only meaningful when testing children. IQ tests began using "deviation IQs" based on relative comparisons of performance between a test-taker against a sample used to norm the test in order to be able to measure adult intelligence, especially David Wechsler's 1939 test. These IQ test scores were fit to a Gaussian distribution because intelligence was assumed to follow such a distribution. Intelligence testing has historically been of interest to eugenicists as a way of identifying who is exceptional and who is defective.

In practice, intelligence in humans is... weird. An IQ test can identify someone who is exceptionally dumb or intelligent, but a person who scores a few points higher or lower is not necessarily "smarter" or "dumber", just able to solve whatever pattern the IQ test is testing; at best the IQ test is the map, not the territory. Richard Feynman scored an IQ of "only" 124, which would put him in the "significantly above average" category but much less than the "genius level" one would expect of a Nobel-prize winning Physicist, or any random physicist for that matter; the average IQ of Physicists is 128. He would not be allowed to join Mensa with that IQ, but he was probably smart enough to notice that anyone bragging about going to such a meeting was advertising the schedule of when their wife would be all alone. Meanwhile, plenty of "geniuses" fail to achieve success and plenty of people with below average intelligence manage to do quite well and establish businesses.

Furthermore, as anyone who has done studies on intelligence can assure you, a penguin scores consistently as highly as non-English speakers.

See also

• The Bell Curve
• Francis Galton
• Probability
• Statistics

References

Mathematics Articles on RationalWiki

-  Hypatia of Alexandria  -  Sophie Germain  -  Rene Descartes  -  Fibonacci sequence  -  Gödel's incompleteness theorems  -  Golden Ratio  -  Pyramid  -  Fermat's last theorem  -  Information  -  Metric system  -  Statistics  -  Conservapedian mathematics  -  Phli (fun)  -  Zero  -  Mathematics  -

v - t - e